|
Le concept de la logique floue vient de la constatation que la variable booléenne, qui ne peut prendre que deux valeurs (vrai ou faux) est mal adaptée à la représentation de la plupart des phénomènes courants. Par exemple, on trouve dans un traité de médecine l'affirmation suivante : un patient atteint d'hépatite présente généralement les symptômes suivants :
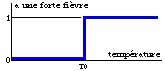 Comment modéliser l'état : "a une forte fièvre" ? La variable booléenne ci-contre tente de représenter cet état. En deçà de la température T0, le patient n'a pas de température. Au delà, il doit consulter !Le problème commence lorsqu'il s'agit de donner une valeur à T0. Doit-on prendre 39 ou 40 degrés ? La notion de fièvre est typiquement une notion floue difficilement modélisable avec l'algèbre booléenne classique, surtout si l'on considère les différences de métabolisme d'un individu à l'autre. La variable "a une forte fièvre" manipulée par la logique floue serait la suivante : 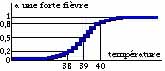 La transition entre les valeurs faux (codée 0) et vrai (codée 1) est maintenant progressive.La fonction représentée doit être considérée comme un degré d'appartenance (degree-of-membership) à l'état décrit ou comme une probabilité d'appartenir à l'ensemble considéré. Ainsi, un patient présentant une température de 38 n'a qu'un faible degré d'appartenance 20 % (0,2) à l'état "a une forte fièvre" alors que celui qui atteint 40 présente un fort degré d'appartenance (80 %) à ce même état. On voit qu'il est maintenant beaucoup plus aisé de fixer la température de basculement (progressif) d'état. A 39 , on n'appartient qu'à 50 % à l'état "a une forte fièvre". Si l'on reprend l'exemple du diagnostic médical, pour un patient dont la température aurait été juste inférieure à la température de transition (38,9 °C pour 39 °C), on aurait exclu l'hépatite alors qu'avec la logique floue, on l'aurait envisagée avec une probabilité moyenne, mais non nulle de 50 % !
On verra qu'il est souvent nécessaire de considérer plusieurs domaines d'évolution d'une entrée ou d'une sortie. Prenons l'exemple de la taille d'un homme : On peut, à coup sûr, classer les hommes suivant leur taille en petit, moyen et grand, mais comment déterminer les limites entre chaque catégorie autrement qu'avec le secours de la logique floue ? Essayons de définir la catégorie petit (en essayant de ne vexer personne !) : Seriez-vous d'accord avec les règles générales et le diagramme d'appartenance suivants ?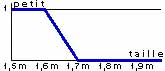 
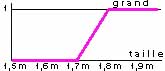
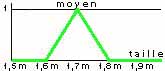
Si l'on superpose les 3 graphiques précédents,
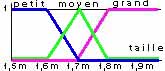 On voit que les courbes se recouvrent.Ce chevauchement est tout-à-fait logique, il montre que lorsque notre taille grandit nous ne passons pas brûtalement d'une catégorie à une autre, mais progressivement. A l'age de l'adolescence, notre degré d'appartenance aux groupes des petits décroit au profit de notre degré d'appartenance au groupe des moyens, et bientôt à celui des grands. Ce chevauchement sera en outre une garantie de stabilité des asservissements basés sur la logique floue.A titre d'exercice, essayez de vous classer dans les 3 catégories, à l'aide du diagramme précédent : Tout le monde regarde ses chaussures de peur d'être interrogeé ! Eh vous là-bas, oui vous le petit râblé qui se cache derrière, quelle taille faites-vous ? Allez, un peu de franchise ! - 1 m 67 ... personne n'est parfait ! Et bien que nous dit le diagramme : Ce n'est pas si catastrophique que cela : vous n'appartenez au groupe des petits qu'à concurrence de 25 % alors que vous êtes déjà moyen à hauteur de 75 %. Désolé, mais vous êtes exclu du groupe des grands avec un degré d'appartenance nul ! Et vous le grand dégingangé, du haut de vos 1 m 82, n'êtes vous pas trop seul dans le groupe exclusif des grands ? Voilà donc présentée la première étape dite de fuzzification des variables. Elle s'applique d'ailleurs aussi bien aux variables d'entrée que de sortie. La puissance à appliquer à un moteur, par exemple, pourra faire appel à des valeurs de puissance telles que "faible, moyenne ou forte". Les courbes d'appartenance prennent différentes formes en fonction de la nature de la grandeur à modéliser : 
Retour à l'introduction   Chapitre suivant |
